本文针对上机时候使用java语言应该掌握的java基础,不断更新中……
并非是详细讲解java基础语法
输入
Scaner scaner = new Scaner (System.in);
//输入数字
int number = scaner.nextInt();
//输入字符串
String string = scaner.next();//不接受下面的符号,也就是输入下面的符号,不会结束当前的输入
String string = scaner.nextLine();//接收回车、换行、TABnext()与nextLine()输入区别
nextInt()、nextFloat()之类函数与next()特性一致。
next()必须先进行有效输入(不包括结束符号的字符)才能结束输入(否则一直是等待输入的状态),然后再使用结束符号结束当前输入(回车、换行、TAB、空格的任一种)nextLine():就没有上面约束了,能接收任何字符,结束符号只有回车一个,所以可以输入含有空格的字符串。
这两个函数的结束符号虽然都有一个回车\n,但是并不一样:
next()接收回车,结束输入后,\n不会消失(要么被下一个next()过滤,要么被下一个nextLine()接收)nextLine()接收回车,结束输入后,会去除掉\n,所以下一个nextLine()可以正常接收输入,而不会接收到回车。
比如我先输入的5,其实输入的是5\n这个\n作为nextInt()结束符,但是\n 并不会消失,如果下面是nextLine() 就会被接收到。
总结一下,这两个输入函数有三点区别:
- 有效输入,
next()必须要接收到有效输入,才能结束输入。nextLine()可以直接接收回车结束字符(实际上接收为空"",因为会自动去除回车)。 - 结束符号种类不同
- 对结束符号
回车的处理不同
格式化输入
OJ有有一种输入是A B,就是两个输入,中间有一个空格。
这种输入在c/c++中很简单scanf("%d %d",a,b);
但java没有格式化输入,可以用nextLine()接收一行数据,然后用string.split(" ")分离开来。也可以直接用next()接收两次,因为空格对next()就是结束符号。
多组数据输入,不确定组数,以EOF结束。
while(sc.haveNext()){
//
}输出
主要是格式化输出:
// 第一种
DecimalFormat df = new DecimalFormat("#0.00");
float data;
data = sc.nextFloat();
System.out.println(df.format(data));
// 第二种,模仿c语言的输出方式,但是不会换行
System.out.printf("%.2f\n", data);// 保留两位小数
System.out.printf("%5d",n);//域宽为5
格式字符 :
% - 0 m.n [类型符号]
①%:表示格式说明的起始符号,不可缺少。
②-:有-表示左对齐输出,如省略表示右对齐输出。
③0:有0表示指定空位填0,如省略表示指定空位不填。
④m.n:m指域宽,即对应的输出项在输出设备上所占的字符数。(如果输出位数少于m位,左端默认补空格,字符数是指整个实数的位置,包括小数点)n指精度。用于说明输出的实型数的小数位数。为指定n时,隐含的精度为n=6位。
⑤[类型符号] d表示整数 f表示浮点数
// 第三种
System.out.println(String.format("%.2f", data));注意一点,OJ输出样例最后一行都没有换行,但实际上需要有一个换行。
基本数据类型
int、float、double、char、String
String不算基本数据类型,应该是类了。
由这些基本数据类型装箱的类对应是Integer、Float、Double、Character。
int 4字节(32bit) -2^31 ~ 2^31 - 1
short 2字节(16bit) -2^15 ~ 2^15 - 1
long 8字节(64bit)-2^63 ~ 2^63 - 1
float 4字节(32bit)2^-149 ~ 2^128 - 1
double 8字节(64bit)2^-1074 ~ 2^1024 - 1
char 1字节
常用的方法
//比较大小
//按字典顺序比较两个字符串。
a.compareTo(b);//如果a>b 返回大于0的数
//类型转换
int Interger.parseInt(String s);
Interger Interger.valueOf(String/int s);
//判断是否是数字
Character.isDigit(String s);进制转化
//其他进制转十进制
Integer.valueOf("[数字字符串]",[进制数]).toString()
//十进制转二进制
Integer.toBinaryString(int i)
//十进制转八进制
Integer.toOctalString(int i)
//十进制转十六进制
Integer.toHexString(int i) 字符的ASCII码
数字0的ASCII码是48,9对应是57
大A对应65,小a对应是97
字符串
取子串
//substring 方法用于提取字符串stringObject中介于两个指定下标[start,stop)之间的字符。stop的位置不会被取到,不写stop,默认到字符串末尾
testString.substring(start,stop);
//没有length,一直取到末尾
stringObject.substr(start [, length ]);
子串查找
返回匹配子串第一个字符在原字符串中的位置
string.indexof(String s);//返回第一次出现的指定子字符串在此字符串中的索引。
string.indexof(String s, int startIndex);//从指定的索引处开始,返回第一次出现的指定子字符串在此字符串中的索引。
lastIndexOf(String str) //返回在此字符串中最右边出现的指定子字符串的索引。
lastIndexOf(String str, int startIndex) //从指定的索引处开始向后搜索,返回在此字符串中最后一次出现的指定子字符串的索引。
?判断是否存在这样的子串
string.contains(String s);字符查找
string.charAt(index)字符数组转换
//char数组转String
char data[] = {'s', 'g', 'k'};
String str = new String(data);
str = String.valueOf(data);字符串构造
//字符串构造
StringBuilder s = new StringBuilder();
StringBuilder s = new StringBuilder(String s);//直接把字符串作为参数
s.append(String s);
s.reverse() //反转序列
s.delete(int start,int end)//移除指定范围字符
s.insert(int offset, i)//在指定位置插入字符或者字符串,可以说包含了append的功能
s.replace(int start, int end, String str)//用新的字符串替换指定序号范围的子字符串
替换
这个替换和StringBuilder类的替换方法不一样,有两点区别:
- String replace方法不会修改自身字符串内容,只是返回一个新的字符串
- StringBuilder 是按范围替换一段新的字符串,String是按字符或者按正则匹配,替换所有匹配上的地方。
string.replace(char a,char b);//把所有的a字符替换成b字符
string.replaceAll(regex, String replace);//根据正则表达式替换集合
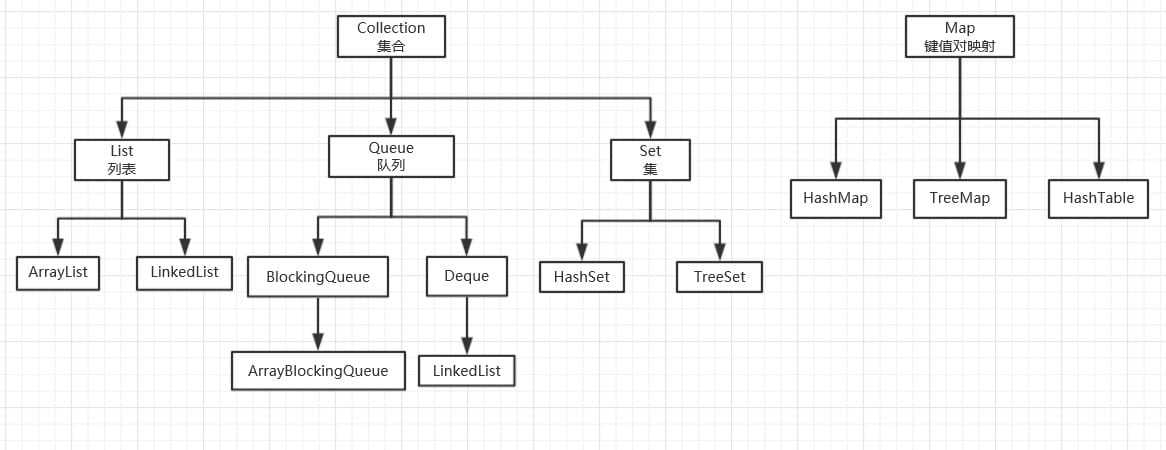
java迭代器的使用
就是用来循环遍历集合的。如果是边循环边根据条件删除元素一定要使用迭代器了,否则会导致删除的不对。
List<String> list = new ArrayList<>();
list.add("*");
list.add("*");
list.add("*");
list.add("*");
for (int i = 0; i < list.size(); i++){
if(list.get(i).equals("*")){
list.remove(i);
}
System.out.println(i + "|" + list.size());//注释代码
}
System.out.println(list);
输出结果是:
0|3
1|2
[*, *]为什么?因为你删掉之后,集合大小就变化了,i还是一直递增的。
直接用迭代器:
for (Iterator iterator = list.iterator(); iterator.hasNext();) {
String string = (String) iterator.next();
if(string.equals("*")){
iterator.remove();
}
}Iterater
hasNext();//如果迭代器指向位置后面还有元素,则返回 true,否则返回false
next();//返回集合中Iterator指向位置后面的元素
remove();//删除集合中Iterator指向位置后面的元素ListIterator
Iterator可以应用于所有的集合,Set、List和Map和这些集合的子类型。而ListIterator只能用于List及其子类型。
ListIterator多了很多有用的方法:
//获取当前元素索引(通过上一个或者下一个元素的索引间接获取):
nextIndex()-1;
previousIndex()+1;
//倒序输出,获取ListIterator,要传递list大小作为参数:
for (ListIterator iterator = list.listIterator(list.size()); iterator.hasPrevious();) {
String string = (String) iterator.previous();
System.out.print(string);
}
//添加元素
add(E e);
//修改元素
set(E e);List
// 建立链表
List<Integer> list = new ArrayList();
//增加数据
list.add(val);
//删除
list.remove(int index);
list.remove(Object object);//需要重写类的equal方法
iterator.remove();
// 指定位置插入数据
list.add(pos,val);//不会覆盖,该位置原来的值以及后面的值都会向后自动移动一位
list.set(pos,val);//会覆盖pos位置的值(修改元素值)
// 查询指定位置的值
list.get(pos);
// 判断某元素值是否存在
list.contains(val);//返回true false
list.indexof(val);//返回第一个匹配项的位置或者-1
// 数组转list
ArrayList<String> list = new ArrayList<String>(Arrays.asList(strArray)) ;
//合并数组
list.addAll(List list2);
//list转数组
String[] sss = listStrings.toArray(new String[listStrings.size()]);
//list转String
循环遍历list,使用StringBuilder的append方法
//排序
Collections.sort(list);// 默认升序
Collections.sort(listCollections.reverseOrder();//降序排序
//自定义排序接口,返回1表示,o1和o2要进行左右交换移动,-1表示不需要移动。0表示两个值相等。
//去除重复元素
list转set再转list
list = new ArrayList<>(new LinkedHashSet<>(list));//这里用LinkedHashSet是因为会保证元素的添加顺序和之前的list一致对集合成员不是基本数据类型的List进行去重?
需要重写hashCode() 和 equals() 方法。
这里必须要保证equals相等的两个元素对应的hashcode也相等。否则set集合不认为这两个是同一个元素,虽然equals返回值为1。
在List.remove(Object e);其实只需要重写equals() 一个函数就可以,当然根据设计规划,两个元素相等,其hashcode()也一定相等,这是一种约定。避免别人用你的代码产生不必要的问题。
https://www.cnblogs.com/dolphin0520/p/3681042.html
set
set好处就是没有重复元素,构造方法上面也可以看出来,可以直接把list转成set
PriorityQueue
java优先队列,每次peek()总是输出一个按照指定规则的的元素(默认是取出最小的)。但是队列内部,并不是有序的。
//实现大顶堆,构建的时候传递Comparator参数
//初始化堆大小随便的,即使是1,也可以不断的添加新元素
Queue<ListNode> priorityQueue = new PriorityQueue<ListNode>([初始化堆大小],new Comparator<ListNode>(){
@Override
public int compare(ListNode o1, ListNode o2) {
return o1.val-o2.val;
}
});//定义
PriorityQueue<Integer> list = new PriorityQueue<Integer>();
//增加元素
list.add(int)
list.offer(int);
//获取队首元素,但不删除
list.peek();
//获取队首元素,且删除
list.poll();栈Stack
栈的特点是先进后出。
Stack 继承自 Vector(动态数组,很多方法和list差不多)
Stack<Interger> stack = new Stack();
stack.isEmpty();//判断栈是否为空
stack.ClearStack:清空栈
stack.size();//即栈的长度
stack.peek();//返回栈顶元素
stack.push();//进栈
stack.pop();//返回栈顶元素,并删除栈顶元素Map
Map并不是简单的二元组,有一个特点是Key不能重复的。
//建立map
Map<Integer,Integer> map = new HashMap<>();
//插入/修改元素
map.put(key,val);
map.putAll(Map t)
// 按照Key 查询
map.get(key);
//删除元素
map.remove(key);
// 按key 排序
(降序排序)
核心就是map转list,然后对list进行排序
// map 转换成 list
Set<Map.Entry<Integer, Integer>> entrys = map.entrySet();//利用这个获得map的键值对映射的集合
List<Map.Entry<Integer, Integer>> = new ArrayList<>(entrys);//list的元素类型就是set<Map.entry<Integer,Integer>> 类型参考文章: https://baike.xsoftlab.net/view/250.html
数组
//定义一个空数组
int [] empty = new int[5];
//定义一个有初值的数组
int [] have = new int[]{1,2,3};Math 类的常用方法
//计算a的b次幂,a^b
Math.pow(double a, double b)
System.out.println(Math.pow(2, 3)); // 8.0
//计算自然常数的a次幂,e^a
Math.exp(double a)
System.out.println(Math.exp(1)); // 2.718281828459045
//计算平方根,√a
Math.sqrt(double a)
System.out.println(Math.sqrt(16)); // 4.0
//计算立方根,a‾√3a3
Math.cbrt(double a)
System.out.println(Math.cbrt(8)); // 2.0
//计算以e为底的对数(自然对数),logexlogex 或 lnxlnx
Math.log(double x)
System.out.println(Math.log(Math.E)); // 1.0
//计算以10为底的对数,log10xlog10x 或 lgxlgx
Math.log10(double x)
System.out.println(Math.log10(100)); // 2.0
//计算绝对值,参数类型:int、long、float、double
Math.abs(int x)
System.out.println(Math.abs(-1)); // 1
//内部调用了 Random.nextDouble() 方法,生成一个伪均匀分布在0.0到1.0之间的double值
Math.random();
System.out.println((int)(Math.random() * 10 + 1)); // 生成范围再[1, 11)之间的伪随机数
//获取两个参数中的最大值,参数类型:int、long、float、double
Math.max(int x, int y)
System.out.println(Math.max(1, 2)); // 2
//获取两个参数中的最小值,参数类型:int、long、float、double
Math.min(int x, int y)
System.out.println(Math.min(1, 2)); // 1
正则表达式
先简单介绍一下:
Patten接收正则表达式作为参数Matcher在Matcher基础上接收字符串作为参数
分割字符串
这个方法是我用的最多的。在处理一些复杂输入中非常有用
//方式1,用String类提供的方法
testString.split([正则表达式],[limit]);
//方式2
Patten p = Pattern.compile("\\d+");
p.split([string],[limit])
/* limit 选填,limit参数控制应用模式的次数,从而影响结果数组的长度。
1. 如果 n 大于零,那么模式至多应用 n- 1 次,数组的长度不大于 n,并且数组的最后条目将包含除最后的匹配定界符之外的所有输入。
2. 如果 n 非正,那么将应用模式的次数不受限制,并且数组可以为任意长度。
3. 如果 n 为零,那么应用模式的次数不受限制,数组可以为任意长度,并且将丢弃尾部空字符串。
*/判断某段在字符串中是否存在以及查找匹配子串的位置
//方式1:Patten 静态方法或者实例方法【完全匹配】
Patten.matcher(String regex,CharSequence input);//返回 true or false
Patten.matches("\\d+","2223");//返回true
Patten.matches("\\d+","2223aa");//返回false
Patten.matches("\\d+","22bb23");//返回false
//方式2:Matcher 类方法
m.matches();//【完全匹配】,和上面效果一样
m.lookingAt();//【部分匹配】。223aa 返回true
//注意:通过m.matches()/m.lookingAt()/m.find() 都会移动指针到下一个匹配的字符串位置,会影响后续的m.find()操作的结果。
m.reset();//重置匹配指针的位置
Matcher m = p.mather(testString);
m.find();//【部分匹配】,返回true or false,而且指针会移动下次匹配的位置
while(m.find()) {
System.out.println("位置1" + m.start());
System.out.println("位置2" + m.end());
System.out.println(m.group());// m.group()返回当前匹配的字符串
System.out.println(m.groupCount());//返回当前匹配的组的数目
System.out.println(m.group(0));//返回当前字符串的第一组的字符串
}上面判断是否存在,以及匹配的字符串是什么,也可以输出匹配字符串在原字符串中的位置。
https://blog.csdn.net/zengxiantao1994/article/details/77803960
ScriptEngineManager
今年看一个大佬的代码才发现java中可以调用JavaScript代码在,并获取其结果。比如一个中缀表达式计算,直接用JavaScript计算就可以了……绝了!
ScriptEngineManager manager = new ScriptEngineManager();
ScriptEngine engine = manager.getEngineByName("javascript");
//根据“脚本语言名称”获取执行引擎,java本身默认只支持javascript
//getEngineByName方法每次都会创建一个新的Engine对象
String script = "3+4*5";
int result = engine.eval(script);
System.out.println(total); https://shift-alt-ctrl.iteye.com/blog/1896690
数据结构和算法
数据结构
树
树的顺序存储结构(父亲表示法)
https://www.ihewro.com/archives/895/#ProblemC 这一题中就用到了这个结构。
这种结构很类似图的临界矩阵的写法。只不过这个是一维结构。
edges[child] = parent每个位置的值为该编号节点的父节点。
public class Tree {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
//n个节点,n-1条边的信息
int [] edges = new int [n+1];//节点编号从1开始
edges[1] = -1;
for (int i = 0; i < n-1; i++) {
int parent = scanner.nextInt();
int child = scanner.nextInt();
edges[child] = parent;
}
for (int i = 0; i < edges.length; i++) {
System.out.print(edges[i] + " | ");
}
System.out.println();
tree_print(edges);
}
public static void tree_print(int[] edges) {
for (int i = 1; i < edges.length; i++) {
System.out.println(i);
for (int j = 1; j < edges.length; j++) {
if (edges[j] == i) {
System.out.print(j + "|");
}
}
System.out.println();
}
}
}
这里mark一下https://www.ihewro.com/archives/894/#ProblemC 的递归KILL 的方法很值得学习。
树的链式存储结构
可以用图的邻接表的结构(孩子表示法)
二叉树
二叉链表结构
https://www.ihewro.com/archives/904/#二叉排序树 这道题目用到这个树的结构,构建树,并且要求前中后遍历打印出来
class TreeNode{
int value;
TreeNode left;
TreeNode right;
public TreeNode(int value) {
this.value = value;
this.left = null;
this.right = null;
}
public TreeNode() {
}
}图
邻接矩阵
https://www.ihewro.com/archives/894/#ProblemD.网络传输
这道题用到了邻接矩阵,同时求图的最短路径,用迪杰斯特拉算法。
class MGraph {
int vertexNum;//顶点数目
int edgesNum;//边的数目
int[][] edges;//二维矩阵,表示任意两个点之间是否有边
}邻接表
堆
堆其实还是二叉树。
算法
迪杰斯特拉最短路径
https://www.ihewro.com/archives/894/#ProblemD
算法目标:求解某个源点O到所有顶点的最短路径
主要思想:
- 集合T,初始状态是除了顶点O之外的所有顶点集合。
- 集合S,初始状态只有顶点O
- dist[],源点到其他所有顶点的距离,初始状态下,初始状态下,如果顶点O与其他顶点直接相连,值就边的权值,如果不相连,值为∞(编程中定义一个很大的数字)
- path[],源点到目标节点的最短路径的前一个节点编号,初始状态下,如果顶点O与其他顶点直接相连,值就是源点O的编号,如果不相连,值为-1
算法过程:
- 每次从T集合吸一个节点到S集合中(吸星大法),这个节点的特征是源点O到该节点的路径长度最小
并使用这个节点作为中间者,修改源点到T集合其他节点(这里只要找T集合的其他节点即可,而不是除源点外的所有节点!!)的最短路径。如果dist[中间点] + 距离△ < dist[其他节点]:
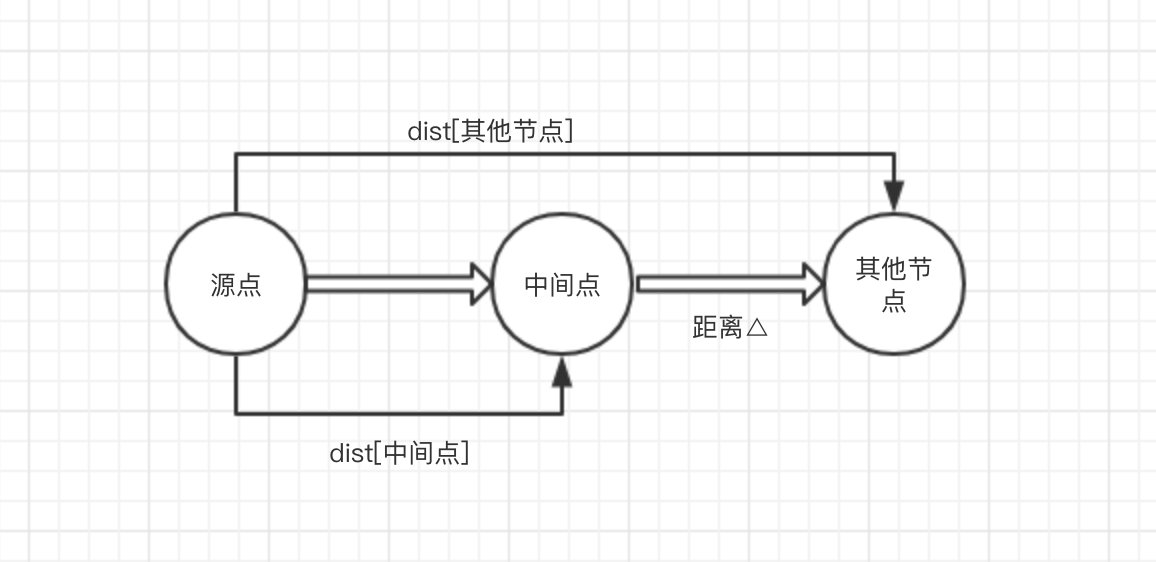
- 修改dist[其他节点] = dist[中间点] + 距离△
- 修改path[其他节点] = 中间点
- 从T集合中移除该中间点
整个过程用一句话就是:不断拿源点到T集合中路径最短的节点作为中间点,修改其他节点的最短路径。
我当初学的时候没明白path[]数组的作用。其实这是一种非常巧妙的存储源点到目标节点路径的方法。
比如:顶点0到顶点6的最短路径是0-1-2-5-4-6
path[6] = 4,只需要存储前一个节点编号就可以,而不需要存储这一串编号。这个思想其实在我们编程中也可以用到。
我们通过path[]数组是怎么找到0到6的完整最短路径的呢?
path[6] = 4
path[4] = 5
path[5] =2
path[2] = 1
path[1] = 0
我们把这些存到栈里面,在出栈就可以了。
java 正无穷表示:通过Double或Float的POSITIVE_INFINITY表示。
负无穷大:通过Double或Float的NEGATIVE_INFINITY表示。
非数字:通过Double或Float的NaN表示。
代码部分
下面代码中没有S集合的定义,因为这个集合在算法中其实没有用。
T集合我用java的list 结构。
图用邻接矩阵的顺序结构表示的。
class MGraph {
int vertexNum;
int edgesNum;
int[][] edges;
int[][] dist;
List<Integer> T = new ArrayList<Integer>();//T集合
public void initEmptyDist() {
dist = new int[vertexNum + 1][vertexNum + 1];
edges = new int[vertexNum + 1][vertexNum + 1];
for (int i = 1; i <= vertexNum; i++) {
for (int j = 1; j <= vertexNum; j++) {
dist[i][j] = -1;
edges[i][j] = -1;
}
}
}
public void Dijkstra(int origin) {
// 1.初始化T集合
for (int i = 1; i <= vertexNum; i++) {
if (i != origin) {
T.add(i);
}
}
while (T.size() != 0) {
int selectVertex = -1;//源点到T集合中顶点最短的路径的顶点编号
int selectVertexInT = 0;//源点到T集合中顶点最短的路径的顶点在T集合中序号,因为后面要从T集合中删掉
int min = -1;//源点到T集合中顶点最短的路径
//2. 选择中间节点
for (int i = 0; i < T.size(); i++) {
if (dist[origin][T.get(i)] != -1 && (dist[origin][T.get(i)] < min || min == -1)) {
min = dist[origin][T.get(i)];
selectVertex = T.get(i);
selectVertexInT = i;
}
}
// 3. 使用中间点修改T集合中其他节点
for (int i = 0; i < T.size(); i++) {
int currentTargetVertex = T.get(i);
int query = query(selectVertex, currentTargetVertex);
if (query != -1) {
int modified = min + query(selectVertex, currentTargetVertex);
if (dist[origin][currentTargetVertex] == -1 || dist[origin][currentTargetVertex] > modified) {
dist[origin][currentTargetVertex] = modified;
}
}
}
//4. 从T集合中删除中间节点
T.remove(selectVertexInT);
}
}
//查询图中两个顶点间的距离
public int query(int start, int end) {
int result = -1;
if (edges[start][end]!= -1) {
result = edges[start][end];
}
return result;
}
}
floyd 最短路径
https://www.ihewro.com/archives/893/#ProblemC
看完了迪杰斯特拉,我恭喜你,这个算法过程要简单一点。
算法目标:求解所有节点到其他所有节点的最短路径
(效果等价于对每个节点使用迪杰斯特拉算法,但是弗洛伊德算法的时间复杂度很高o(n³))
主要思想:
- dist[][],任意两个节点的最短路径的值,初始状态就是图中两个节点边的值,初始状态就是临界矩阵
- path[][],任意两个节点的最短路径的前一个节点,初始状态所有值为-1,表示没有中间点(这个初始值和迪杰斯特拉不一样)
可以看到,这里没有S集合和T集合了。那中间点是怎么选择的呢?
算法过程:
- 把每个顶点作为中间顶点,然后比较disti 与 disti+distk 判断是否修改最短路径。
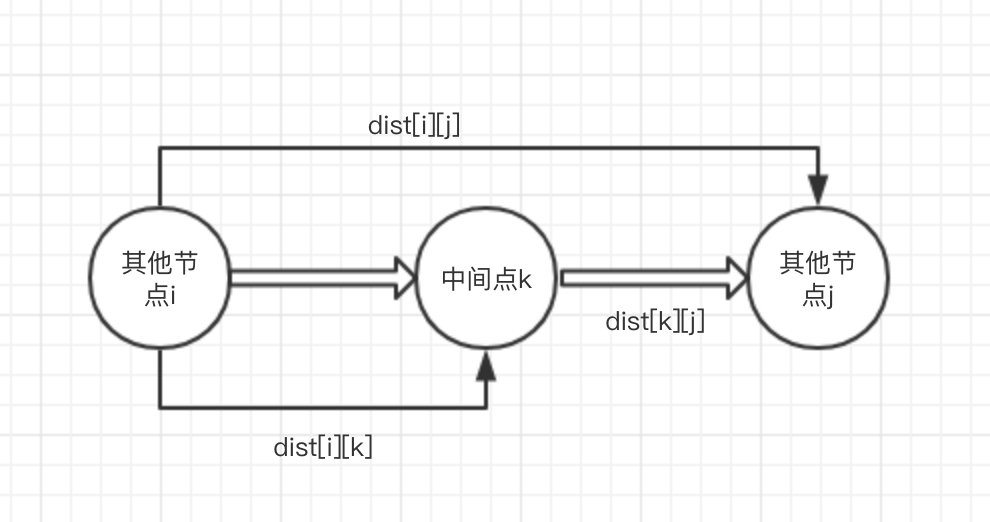
代码:
仍然使用临界矩阵作为图的存储结构。
MGraph mGraph = new MGraph();
//给图赋值代码省略
//1.初始化dist[][]数组
mGraph.initA_array();
//2. 三重循环,把每个顶点作为中间点
for (int i = 1;i<= mGraph.getVertexNum(); i++){// circle each vertex as an intermediate point
for (int k=1;k <= mGraph.getVertexNum();k++){
for (int j = 1;j <= mGraph.getVertexNum();j++){
if (mGraph.A[i][j] > mGraph.A[i][k] + mGraph.A[k][j]){
mGraph.A[i][j] = mGraph.A[i][k] + mGraph.A[k][j];
}
}
}
}
class MGraph{
int vertexNum;
int edgeNum;
int edges[][] = new int[51][51];
int A[][] = new int[51][51];//就是dist[][]
//实例化图的时候,需要先将任意两个节点的边赋值为-1
public MGraph() {
for (int i = 0;i<51;i++){
for (int j = 0; j< 51;j++){
edges[i][j] = -1;//init edges array
}
}
}
//初始化dist数组,等价于edge[][]邻接矩阵数组
public void initA_array(){
for (int i = 1;i<=this.getVertexNum();i++){
for (int j = 1;j<=this.getVertexNum();j++){
if (edges[i][j] == -1){//两个节点没有边
A[i][j] = this.vertexNum;//把节点数作为不可达,因为两个几点的距离不可能超过节点数的大小
}else {
A[i][j] = edges[i][j];
}
}
}
}
}全排列
c++内置全排列算法,羡慕。
permutation(list, 0, list.size() - 1);
public void permutation(List<Integer> list, int from, int to) {
if (to < from)
return;
if (from == to) {
//此时list是一个新的排列
} else {
for (int i = from; i <= to; i++) {
swap(list, i, from);
permutation(list, from + 1, to);
swap(list, from, i);
}
}
}
public void swap(List<Integer> s, int i, int j) {
int tmp = s.get(i);
s.set(i, s.get(j));
s.set(j, tmp);
}eclipse 设置
代码提示
窗口(Window(窗口) > Preferences(偏好设置) > Java > Editor(编辑器) > Content Assist(内容辅助))
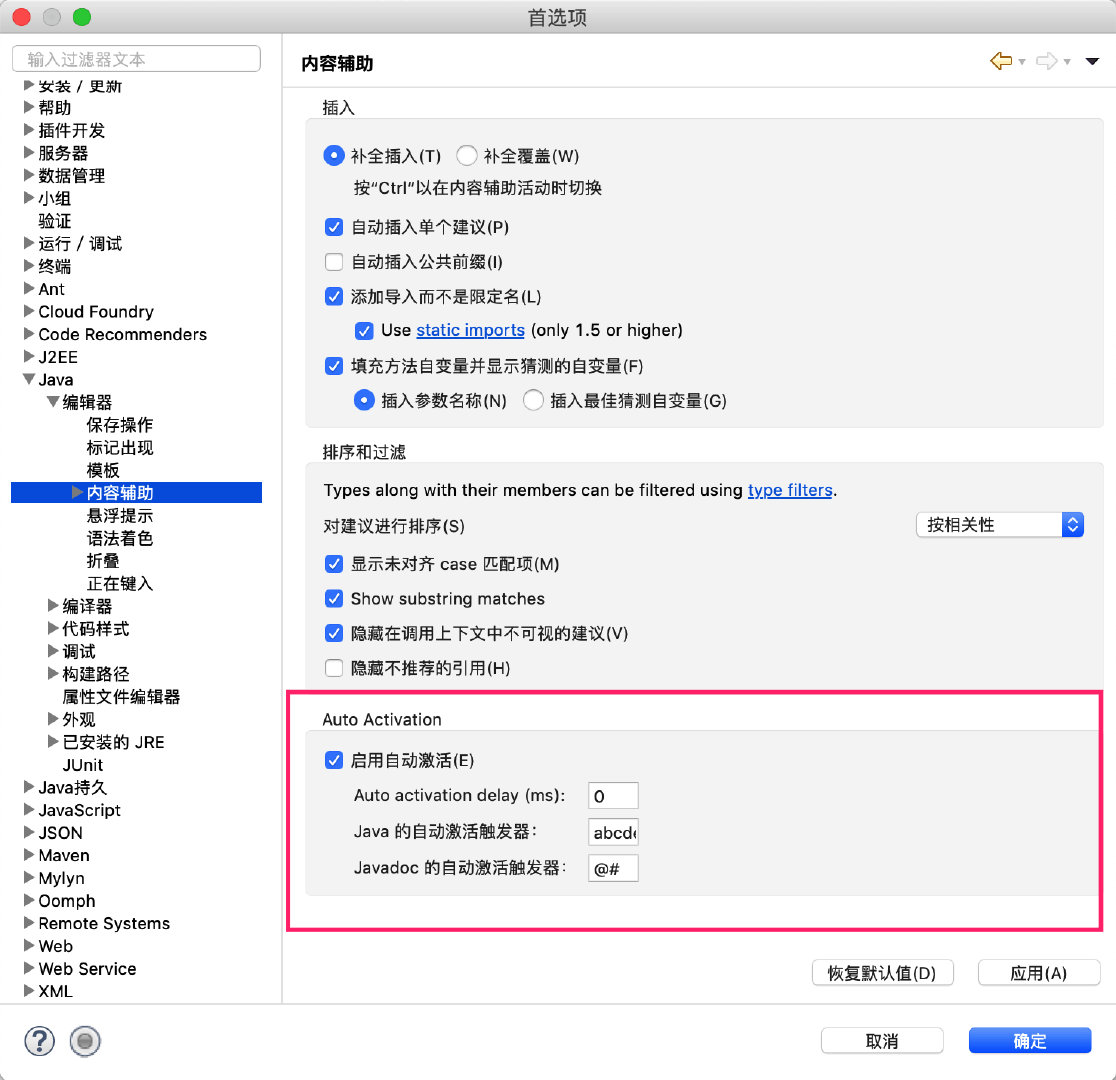
把.修改成.abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ(,
https://blog.csdn.net/ithomer/article/details/7090405
eclipse 常用快捷键
// command = ctrl (windows)
Alt + / 提示
command + / 当行注释
command + d 删除当前行
command + 1 快速修复
syso : System.out.println();OJ常见问题
样例正确,AC失败
- 特殊样例没有考虑到,比如2014网研分数加法第一题
- 复制过去代码不要有包名
package bupt;他不提示编译错误,但是答案就是错误... - 首先确定自己是否正确理解题意
- 然后测试临界条件,特殊条件
- 运行时错误:内存超限,并不是某个数组或集合取数超限,而是内存超限
一些注意的地方
- 变量初始化位置要注意,如果写在循环内部和循环外部就差远了
- 注释在AC成功之前不要删掉,否则后面还得重新加注释……
== 和 equals 使用区别
- 对于
==如果作用于基本数据类型的变量,则直接比较其存储的 “值”是否相等;如果作用于引用类型的变量,则比较的是所指向的对象的地址 对于equals方法
如果没有对equals方法进行重写,则比较的是引用类型的变量所指向的对象的地址;
诸如String、Date等类默认对equals方法进行了重写,比较的是所指向的对象的内容。
注意:equals方法不能作用于基本数据类型的变量。
北邮OJ上机注意点
- 北邮支持c/c++/java7 (我选的是java)
- java 提交代码时候,记得删掉包名,类名称改为Main,入口函数为
main(String[] args); - 提交代码的界面:
- 检查结果的界面: (答案错误,没有任何提示!)
- 不要有中文注释,不支持中文编码

3 条评论
取ASCII最方便的方法就是转char再转int(JAVA小白一个)

是的~但是还是要记住常见几个边界的ascii,在判断是否是数字还是字符的时候有点用户~
记不住的话,可以try,catch包一下